¿Cómo se sabe lo que se sabe? El tamaño de la Tierra, primera parte.
Antes de que empieces a leer esta entrada, un pequeño prólogo.
Una de las cosas que más me suelen despertar la curiosidad cuando leo algún libro sobre ciencia -bien sea de divulgación científica, de historia de la ciencia y de los científicos, o simplemente un libro de texto- o cuando veo algún programa sobre ciencia en la televisión, es cómo se genera el conocimiento científico. En numerosas ocasiones se nos ha mostrado la historia, muchas veces apasionante, que se esconde detrás de los descubrimientos, pero pocas veces se nos dice cómo se realizaron dichos descubrimientos. Es decir, me interesa el experimento con el que finalmente se descubrió algo. ¿Cómo se las apañaron para descubrir esto o para medir aquello? Se nos dice que la velocidad de la luz es tanta, que el planeta Tierra pesa tanto, que la distancia entre la Tierra y el Sol es no se cuánta, que el ángulo entre los dos enlaces de la molécula de agua es tal. A mí esto siempre me deja con una intriga que muchas veces no se resuelve, que consiste en saber cómo se pueden averiguar este tipo de cosas. ¿Cómo se puede pesar la Tierra? ¿Cómo se puede medir la distancia entre el planeta Tierra y el Sol? ¿Cómo sabemos de qué está hecha tal o cual estrella? ¿Cómo sabemos que hay átomos? ¿Y cómo sabemos que los átomos están hechos de protones, neutros y electrones? ¿Cómo, en fin, se sabe lo que se sabe?
Hace ya un tiempo que le vengo dando vueltas a la idea de escribir sobre el tema, de hacer un recopilatorio de las técnicas y experimentos con los que los humanos nos las hemos apañado para medir y para averiguar características de nuestro universo que no son necesariamente obvias a simple vista. Esto que estás a punto de empezar a leer es un primer experimento que voy a hacer sobre este proyecto, a ver qué tal sale. Hablaré de los experimentos históricos que llevaron a descubrimientos singulares y también de las técnicas contemporáneas que sirven para refinar dichos experimentos. Lo haré concentrándome, como he dicho antes, en los experimentos en sí y en el proceso de medida y descubrimiento, más que en la historia del descubrimiento.
Mi intención es hacer un par de entradas piloto para el blog, a ver cuánto esfuerzo y cuánto trabajo me suponen, y cuánto tiempo libre me quitan. También quiero ver el éxito y la recepción que tiene entre vosotros, astutos lectores. Si veo que la cosa tiene mucho éxito y me vitoreáis lo suficiente igual escribo algo más. Sobre todo hablaré de Física, que es de lo que sé un poco, pero si tenéis curiosidad sobre algún tema en particular (¿cómo harán los científicos para saber esto o aquello?) intentaré satisfacer vuestros caprichos. Lo más probable es, que sea lo que sea lo que me preguntéis, no lo sepa, así que habrá que tener paciencia mientras yo aprendo también antes de escribir.
De momento no me enrollo más y os dejo con la primera entrega piloto de esta serie titulada ¿cómo se sabe lo que se sabe? dedicada a la medida del tamaño de la Tierra. ¿Cómo sabemos lo grande que es nuestro planeta? Allá vamos.
¿Cómo se sabe lo que se sabe? Hoy: la medida del tamaño de la Tierra.
Dejemos las cosas claras desde el principio: el tamaño importa. Importa mucho, e importa desde siempre. Tanto es así que la humanidad empezó hace un montón de siglos a intentar averiguar cómo de grande es nuestro planeta, posiblemente por necesidades comerciales y de planificación de rutas por parte de los mercaderes, o por llenar los ratos de copioso asueto de los ricachones. Hoy en día a todos nos cuentan en el colegio más o menos la misma cantinela de que la Tierra es una esfera achatada por los polos que tiene un radio medio de 6371 Km. Esto del radio medio es porque, al no ser nuestro planeta una esfera perfecta, la distancia del centro a la superficie depende de en qué punto de la misma nos encontremos: es mayor la distancia desde el centro de la Tierra a cualquier punto del Ecuador que la distancia de la Tierra a cualquiera de los dos polos. ¿Cómo se llegaron a saber estas formas y tamaños? La historia de la medición del tamaño y forma de la Tierra se remonta, como poco y que se sepa, hasta la Grecia clásica. Si hay una cosa que tenían clara los antiguos es que la Tierra era muy grande y que la cosa no iba a ser fácil ni directa: nada de tirar una cuerda desde aquí hasta allí y ver cómo es de larga, o de viajar dando la vuelta al globo y ver cuánto tiempo nos toma, de modo que tuvieron que inventar sistemas ingeniosos, ayudándose de sus muy buenos conocimientos de geometría, en particular de trigonometría. Para los propósitos de esta entrada, trigonometría es simplemente una rama de las matemáticas que relaciona los lados de un triángulo rectángulo con sus ángulos (y un triángulo rectángulo es uno que tiene un ángulo recto… y un ángulo recto es el que surge de dividir una circunferencia en cuatro ángulos iguales: el ángulo que forma la pared de una habitación normal con el suelo, vaya).
Por cierto, eso de que la gente se pensaba que la Tierra era plana hasta que llegó Colón y demostró que era redonda es un camelo, mentira. Dentro de unos minutos veremos como ya en la época de la grecia clásica había un buen número de filósofos -y gente de otras profesiones posiblemente también- que estaban bastante convencidos de que la Tierra era una esfera. De hecho, el propio Pitágoras, famoso por su teorema, un tipo que vivió en el siglo VI antes de nuestra era, dedujo que la Tierra era esférica porque, si la esfera era el sólido perfecto, el que más le gustaba él y a muchos de sus colegas, ¿cómo era posible que los dioses hubiera creado a la Tierra con cualquier otra forma imperfecta no esférica? Pues eso, obvio.
La medida de la Tierra, como digo, es un tema que lleva preocupando a los humanos prácticamente desde siempre, así que tendremos que remontarnos mucho tiempo atrás para ver cómo se averiguaron la forma y tamaño de la Tierra. Vamos a hablar de tres experimentos clave en la historia de la Geodesia, que es la rama de las matemáticas aplicadas que se dedica a medir nuestro queridísimo planeta. Nuestro viaje comenzará en la Grecia clásica, con la famosa medida de la circunferencia de la Tierra por parte de Eratóstenes de Cirene. Después daremos un salto en el tiempo para aterrizar en el mundo islámico medieval y ver qué estrategia siguió Al-Biruni para medir el radio de la Tierra. Tras Al-Biruni viajaremos de nuevo en el tiempo para aprender sobre el trazado del meridiano de París en el siglo XVIII, y sobre las mediciones que confirmaron que la Tierra es bastante parecida a una esfera achatada por los polos. Finalmente, acabaremos describiendo un par de técnicas contemporáneas para medir distancias y posiciones sobre la Tierra. Ni que decir tiene que no es mi intención hacer un repaso exhaustivo de todas las mediciones y técnicas de la historia, sino contaros una batallita con la que os pueda explicar las técnicas que se han utilizado en el pasado para tomarle la medida al planeta. ¿Listos? Doncs, comencem!
La medida de Eratóstenes
Eratóstenes (276-194, antes de nuestra era) nació en Cirene, una ciudad griega que se encontraba en lo que hoy es Libia. Como muchos otros personajes de su tiempo, sabía hacer un poco de todo: era matemático, geógrafo y astrónomo. Era lo que posiblemente hoy llamáramos un artista o una figura del toreo. Seguramente su aportación más famosa y por la que se le recuerda más sea la medición de la circunferencia de la Tierra que veremos a continuación. La medida del tamaño de la Tierra por parte de Eratóstenes es quizá la medida anterior a la edad moderna más conocida de todas. Una búsqueda en Google de términos como «medida circunferencia Tierra» -sin especifiar nada sobre Eratóstenes ni nada- os dará, mayoritariamente, entradas en las que se explica la medida del de Cirene.
Creo que la primera vez que supe de él y su medida fue viendo la mitiquísima serie Cosmos de Carl Sagan. Cómo olvidar, en el primer capítulo de la serie, la afable y sonriente figura de Sagan, con su jersey rojo de cuello alto y su chaquetilla de pana, explicando desde Egipto, con un mapa de papel con dos obeliscos pegados en él, el experimento de Eratóstenes. Ahora os la explicaré yo a mi manera.
Siendo una medida tan antigua, y con una popularidad tan grande, el experimento de Eratóstenes está rodeado de un halo de leyenda, y muchas veces es difícil distinguir los datos reales, lo que pasara en realidad, de lo añadido a posteriori. Dice esta leyenda que a oídos de Eratóstenes, que por entonces vivía en Alejandría, al Norte de lo que hoy es Egipto, en la costa mediterránea y cerca del río Nilo, llegó la información de que en cierta ciudad hacia el Sur, también en la ribera del Nilo, llamada Siena -hoy Asuán– ocurría un fenómeno muy curioso. Una vez al año, en un día muy concreto, a mediodía, cuando el Sol estaba en lo más alto en su trayectoria por el cielo, se observaba que la luz solar podía llegar al fondo de un pozo. Esto implicaba que el Sol tenía que estar directamente encima del pozo, y que su luz incidía perpendicularmente a la superficie de la Tierra porque de no ser así las paredes del pozo hubieran proyectado su sombra en el fondo del mismo (ver Figura 1) . Del mismo modo, un palo clavado verticalmente en el suelo no proyectaba sombra ninguna. Esto pasaba el día del solsticio de verano gracias a que Siena estaba cerca del Trópico de Cáncer. Vale, ya sé que lo sabéis todos, pero por repasar: el solsticio de verano es precisamente el momento en que el Sol incide perpendicularmente sobre el Trópico de Cáncer, y el momento del año en que el Sol alcanza su máxima altitud en el cielo para todos los que vivimos más al Norte de dicho trópico. En cambio, en Alejandría no pasaba nada de eso. En Alenjandría, al igual que en el resto del hemisferio norte, aunque el Sol también alcanza su punto más alto en el cielo en el solsticio de verano, este punto no es tan alto como para que la luz del Sol entre hasta el fondo de los pozos de agua, o para que un palo clavado verticalmente en el suelo no proyecte sombra ninguna. Es decir, en Alejandría el Sol nunca está tan alto en el cielo como para estar en el punto más alto posible, el cenit, dejando caer sus rayos perpendicular e implacablemente sobre las calvas de los pobres alejandrinos. ¿Cómo se puede explicar que algo así ocurra? ¿Cómo puede ser que el mismo día y a la misma hora las cosas tengan sombra en Alejandría y no la tengan en Siena?
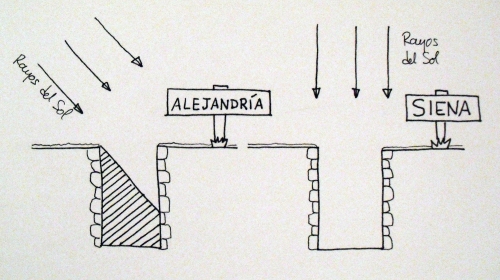
Figura 1. En el solsticio de verano los rayos del Sol inciden con un ángulo determinado sobre Alejandría y perpendicularmente el suelo en Siena, de modo que el fondo de los pozos de Siena son iluminados por la luz solar.
Si pensamos, como Eratóstenes, en que la Tierra es redonda, todo tiene perfecto sentido. Carl Sagan, con su jerselito rojo, pondría su mapa de Egipto con dos obelisco plantados, y nos demostraría que si la Tierra fuera plana, la sombra que producen los dos obeliscos, uno en Alejandría y el otro en Siena, tiene que ser igual: o bien hay sombra en ambos lugares, o no la hay en ninguno de los dos. Sin embargo, si la superficie de la Tierra es curva -cosa que Sagan demostraba curvando el mapa- las sombras que producen los dos obeliscos ya no son iguales. Este hecho fue del que se aprovechó Eratóstenes para su famoso experimento. Si en el mismo instante en que un palo calvado en el suelo de Siena no produce ninguna sombra, yo, en Alejandría, mido la longitud de la sombra de un palo vertical, puedo deducir fácilmente el ángulo entre los dos palos, el mío en Alejandría y el de un amiguete en Siena (ver Figura 2). Conociendo el ángulo entre los dos palos, y sabiendo también que al estar ambos clavados verticalmente en el suelo, sus prolongaciones (imaginarias, claro) hacia el subsuelo se unen exactamente en el centro de la Tierra, puedo saber a qué proporción de la superficie de la Tierra corresponde la distancia entre Alejandría y Siena. Ahora viene el cálculo, que en el fondo no es sino una regla de tres. Si yo sé que el ángulo entre los dos palos de mi experimento es una cierta fracción de 360º (es decir, una cierta fracción de la circunferencia completa de la Tierra), la distancia entre Alejandría y Siena es esa misma fracción de la longitud de la circunferencia de la Tierra. Ya tenemos la teoría lista y el experimento diseñado. Ahora vamos a la práctica.
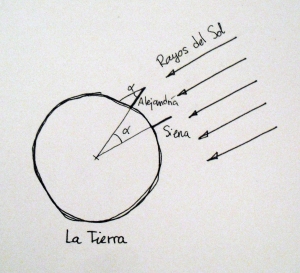
Figura 2. Esquema del planeta Tierra, con los palos verticales clavados en el suelo de Alejandría y Siena y sus prolongaciones hacia el centro de la Tierra. En el solsticio de verano, el ángulo que forman los rayos del Sol con el palo de Alejandría es igual al ángulo entre los dos palos.
La leyenda detrás de este experimento se vuelve ahora aún más legendaria. Se dice que Eratóstenes pagó (o simplemente obligó, vete a saber) a alguien para que fuera caminando de Alejandría a Siena y viera cómo de lejos estaba una de la otra. Incluso he llegado a leer por ahí que esta persona -a la que hoy posiblemente llamaríamos becario de Eratóstenes- fue de Alejandría a Siena caminando junto a un carro, contando las vueltas que daba la rueda del mismo, para de ahí (sabiendo el radio de la rueda del carro, es decir, la distancia entre el eje de la rueda y el borde de la misma) calcular cuánto avanza el carro por cada vuelta de rueda, y con el número total de vueltas que contabilizara, averiguar la distancia. Me parece más probable, sin embargo, que Eratóstenes se valiera de mediciones de la distancia entre Alenjandria y Siena que hubiera hecho otra gente antes que él, aunque seguiré refiriéndome a su becario porque posiblemente tuviera uno y porque seguramente las medidas anteriores que utilizó Eratóstenes fuera realizadas con ayuda de becarios. Sirva esto como homenaje a los becarios del mundo.
Mientras el becario de Eratóstenes mide la distancia entre Alejandría y Siena, nosotros nos quedamos con su jefe, el día del solsticio de verano, midiendo la longitud de la sombra de un palo clavado verticalmente en el suelo, para de ahí calcular el ángulo del palo con respecto a los rayos del Sol (que, recordemos, son paralelos a un hipotético palo clavado verticalmente en Siena). ¿Que cómo se calcula esto? La terminología y las unidades en los tiempos de Eratóstenes probablemente fueran diferente de las de hoy en día, pero la esencia es la misma. Hay dos maneras básicas, al menos, mediante las que se puede realizar el cálculo. En la primera estrategia consideramos el triángulo cuyos tres lados son el palo clavado verticalmente sobre el suelo de Alejandría, la sombra del palo a mediodía del solsticio de verano, y la línea imaginaria que une el extremo del palo con el extremo de la sombra, y que es paralela a los rayos del Sol y al palito de Siena (ver Figura 3). Ahora tenemos que hacer uso de la función trigonométrica llamada tangente, que relaciona la longitud del palo y la de la sombra con el ángulo entre el palo y los rayos del Sol (que es lo que queremos saber), y que se define como tan(Q)=S/P, es decir, la tangente del ángulo es igual a la longitud de la sombra dividida entre la longitud del palo. A partir de ahí, con una calculadora, podemos calcular el ángulo. La otra manera de averiguar el ángulo entre los rayos del Sol y el palo es hacer una medida directa: se ata el extremo de un cordel a la punta del palo, y el otro extremo se sujeta en el suelo, justo sobre el extremo de la sombra del palo. Entonces, con algún aparato para medir ángulos, un transportador de ángulos suficientemente grande o algún dispositivo similar, se mide el ángulo entre el palo y el cordel.
Eratóstenes calculó que el ángulo entre su palito y el de Siena -que, perdonad que me repita tanto, es el ángulo entre el radio que conecta el centro de la Tierra y Alejandría y el radio que conecta el centro de la Tierra con Siena- es 1/50 de la circunferencia de la Tierra. Esto quiere decir que si el ángulo entre el radio que pasa por Alejandría y el que pasa por Siena es de una cincuentava parte de la circunferencia total, la distancia entre Alejandría y Siena medida por la superficie de la Tierra es también una cincuentava parte de la circunferencia total de la Tierra. De modo que en cuanto el becario de Esratóstenes vuelva de Siena con la medida de la distancia entre las dos ciudades, podremos saber la medida de la circunferencia de la Tierra.
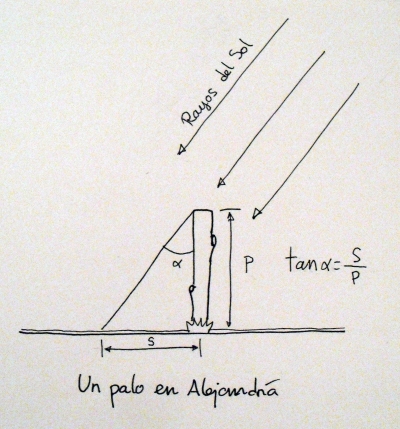
Figura 3. Triángulo utilizado para averiguar en ángulo α, que es el mismo que el ángulo entre los palitos de Alejandría y Siena. Incluyo la fórmula de la tangente de α, que es igual a la longitud de la sombra dividida por la lontigud del palo.
Aquí la leyenda de Eratóstenes pierde un poco de solidez por una cuestión de unidades de medida. Sabemos que la medida de la distancia Alejandría-Siena del becario de Eratósnes fue de 5 000 estadios, de modo que la circunferencia total de la Tierra sería de 250 000 estadios pero ¿cuántos metros son un estadio? Pues no lo sabemos bien. Algunos estudiosos son partidarios de pensar que el estadio al que se refería Eratóstenes era el egipcio, de 157.5 metros de los de hoy en día, con lo que la medida de la circunferencia de la Tierra sería de 39 690 km, solamente un 1.6% alejada del valor que conocemos hoy de 40 075 km. Otros, como Dennis Rawlins, creen que esto es un exceso de celo idealizador de algunos fans de Eratóstenes, y que no hay justificación para pensar que el estadio que utilizaron era de 157.5 m, sino de 185 metros (que es prácticamente la décima parte de una milla náutica), con lo que el error sería del 16% aproximadamente. A esto hay que sumar que para que esta medida sea precisa, Alejandría y Siena tendrían que estar sobre el mismo meridiano: estar situadas en una línea que apunte exactamente entre el norte y el sur. Dicho de otra manera, tendría que ser mediodía exactamente a la misma hora en las dos ciudades. Sin embargo, no es así, con lo que que la medida del becario de Eratóstenes nos da una sobreestimación de la circunferencia de la Tierra. Aún así, lo ingenioso y elegante de la medida, de la planificación del experimento, merecen en mi opinión que la leyenda de Eratóstenes se conserve, eso sí, sin olvidar que Eratóstenes, como todos los científicos del mundo, se valió de lo que otra gente había hecho antes que él.
Apéndice
Pero, ¿y si al final Eratóstenes resulta que no hizo este experimento? ¿Entonces qué valor tiene todo esto que cuento aquí? Desde el punto de vista de mis objetivos, tiene todo el valor. A mí lo que me interesa es contar maneras de descubrir cosas que no son ovbias a simple vista. Este experimento en sí es una idea ingeniosa, brillante y que se puede repetir en cualquier momento para medir nosotros mismos el tamaño de la Tierra, especialmente hoy en día que se puede uno comunicar en tiempo real con cualquier lugar del globo. ¿Que tienes un colega que vive en la otra parte del mundo? Pues quedáis un día, hacéis una vídeo llamada y medís la sombra que proyecte un palo vertical en cada lugar. De hecho hay muchísima gente que ha replicado este experimento o alguna variante y cuenta su historia en internet (por ejemplo aquí), y también hay bastantes proyecto educativos en los que se llama a los chavales de colegios e institutos a que hagan su propio experimento o demostración y lo suban a Internet (por ejemplo estos dos), cosa que me parece una ídea magnífica.
Para saber más
Si queréis saber más sobre cómo se miden las distancias, alturas y posición de los objetos sobre la superficie de la Tierra, os recomiendo que echéis un vistazo a estas fuentes, que son en las que me he basado para escribir esta parte.
Capítulo 1 de Measuring the Universe. The historical quest to quantify space, Kitty Ferguson, Headline Book Publishing, London, 1999. Hay una traducción el español: La Medida del Universo, Ed. Ma Non Troppo, 2000.
¿Cómo Eratóstenes midió la circunferencia de la tierra hace 2 mil años?
Los artículos de Wikipedia sobre la Geodesia y su Historia. Pongo los enlaces a la Wikipedia en inglés porque suele estar mucho mejor que la versión en español.
El vídeo de Cosmos con la expicación de Carl Sagan.
Este artículo donde se discute cuánto hay de leyenda (según los autores parece que mucho) y cuánto de cierto (según los autores parece que no demasiado) en la leyenda detrás de esta medida.
On the importance of spectral match when characterising organic solar cells
Photovoltaic devices are usually characterised using simulated sunlight. A solar simulator consists essentially on a light source, often a Xe arc lamp, and a set of filters with the aim that the spectral distribution of the emitted light is as close as possible to the standard AM1.5g spectrum, and its integrated intensity is 1000 
In the day-to-day lab life, setting up your experiment so it matches these two requirements (spectral distribution and integrated intensity) is done by first, getting an spectral-class A solar simulator to have the peace of mind that the spectral distribution of the emitted light is quite close to the AM1.5g spectrum and, second, using a calibrated reference solar cell to set the intensity of the lamp in your simulator and the distance between the simulator and your devices so the light intensity that reaches the cells is 1000
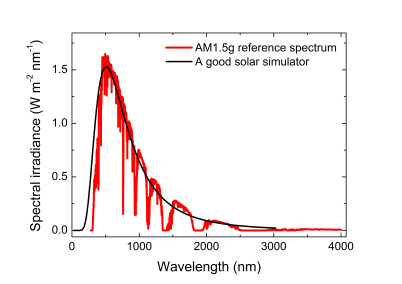
Figure 1. Spectral irradiance of the AM1.5g standard solar spectrum (red) and of an ideal solar simulator, produced with a 5700 K blackbody irradiance spectrum (black).
Spectral class A means that the integrated intensity of the light emitted by the solar simulator falls within 
To verify that, in addition to having the correct spectral shape, the light intensity falling on the solar cell under test is actually 1000 
Most often, Si solar cells are used as reference cells and that is mostly fine whenever the devices under study have a spectral response similar to that of Si solar cells, especially in terms of energy band gap , which for Si is around 1100 nm. However, when characterising organic cells, which tend to have larger energy band gaps, using a Si reference cell can lead to large measurement errors. In the following paragraphs I will try to illustrate how these errors can arise.
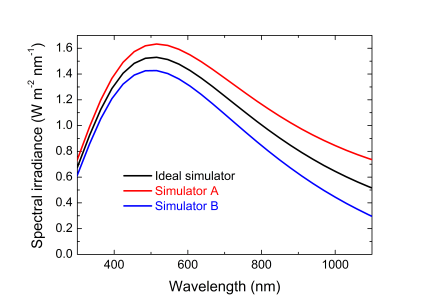
Figure 2. The ideal simulator of Figure 1 (black) and two slightly different simulator A (red) and B (blue).
Let’s assume that we want to compare the results be obtain with the ideal solar simulator of Figure 1, with what two other research groups A and B get using their solar simulators, which have slightly different emission spectra in the range of interest (300-1100 nm for a Si reference cell). For the record, I have produced these two spectra by adding a straight line with a positive/negative slope to the emission spectrum of the ideal simulator (Figure 2).
In a real situation, we would set the lamp intensities and simulator-cell distances so the Si reference cell yields in all three labs the same
Figure 3. External quantum efficiency of a Si solar cell (black) and of the same cell under a KG5 optical filter (red).
Now that the systems are set up, let’s characterise our organic solar cell. Let’s assume, for example, that it is based on PTB7 polymer, whose energy band gap is something around 750 nm. Our organic solar cell only sees light from 300 to 750 nm, and is transparent from roughly 750 nm onwards. This is illustrated with a yellow-shaded area in Figure 4. How close to each other (and to the ideal simulator and the AM1.5g standard, for that matter) are both simulators A and B in terms of the emission spectrum in the relevant range? Figure 4 shows the spectrum of Simulator A is below that of Simulator B on the whole range considered, i.e. there is a clear bias in favor of Simulator B even though all simulators were calibrated with a Si cell to give 1000 
Figure 4. Spectral irradiance of the three solar simulators (ideal in black, A in red and B in blue) after intensity normalisation using a Si reference cell. The spectral region relevant for PTB7-based solar cells is highlighted in yellow.
To solve or at least minimise this discrepancy, there are several strategies that can be followed. One of them is the use of the so-called mismatch factor. This is a factor that results from comparing the short circuit current that the device under test and the reference cell would give when illuminated by the AM1.5g standard on one hand and by a particular solar simulator on the other. This factor can be multiplied to the
Another, quite practical way of reducing the mismatch errors consists on using a reference cell for the calibration of the solar simulator lamp intensity that is better suited for the particular device under test. As said above, the mismatch factor compares the light sources and also the spectral responsivity of the reference and test cells. The former is something about which labs normally cannot do much: once you buy your Class A solar simulator, that’s about it unless you can get a new filter that makes its emission spectrum even closer to the AM1.5g standard. However, if the spectral responsivity of your Si solar cell is not similar to that of the device you are trying to characterise, you can always use a different reference cell whose spectral responsivity matches better that of your device. This results in a experimental setup whose mismatch factor is closer to unity.
A usual alternative reference cell employed often -but by no means always- in the organic photovoltaic community is a Si reference cell with a KG5 optical filter that basically elminates any light of wavelenghts above 750 nm, the light not seen by PTB7-based devices. Using such a cell to set the intensity of our simulators A and B, again by multiplying the emission spectra by the EQE of the KG5-filtered reference cell (red line in Figure 3), integrating, and adjusting the intensities until all simulators give the same
Figure 5. Spectral irradiance of the three solar simulators (ideal in black, A in red and B in blue) after intensity normalisation using a KG5-filtered Si reference cell. The spectral region relevant for PTB7-based solar cells is highlighted in yellow.
Is using a calibrated, KG5-filtered reference cell the optimal solution? Well, depends on the particular solar simulator and device under test. If your simulator is excellent and matches perfectly the AM1.5g spectrum, just like the ideal one of Figure 1, it would not matter what reference cell you use, although finding such a solar simulator is not a trivial task. If your simulator is not perfect, using a KG5-filtered Si solar cell will improve your mismatch factor, but may not be enough to make it exactly equal to unity. On the other hand, a KG5-filtered calibrated solar cell is useful if its spectral responsivity is close to that of the device under test. Otherwise, another reference whose spectral responsivity matches the device under test has to be found (like, for example, a Si cell filtered with a different optical filter).
References and further reading.
The spectral mismatch factor. Application Note 51 and Simulation of Solar Irradiation by Newport Corporation.
Toward reliable and accurate evaluation of polymer solar cells based on low band gap polymers, Long Ye et al., J. Mater. Chem. C, 3, 564 (2015)
Measurement and Characterization of Solar Cells and Modules, by K. Emery, in Handbook of Photovoltaic Science and Engineering, eds. A. Luque and D. Hegedus, John Wiley and Sons, West Sussex (2003)
Accurate Measurement and Characterization of Organic Solar Cells, V. Shrotriya et al., Adv. Funct. Mater., 16, 2016 (2006)
The Túzaro 
leave a comment